Blog
6 min read

Deep Learning using Quantum Annealers

By Team Algo

Reading Time: 6 minutes

By Amey Patil, Associate Data Scientist at AlgoAnalytics

Using D-Wave’s Quantum Annealer for pre-training of Deep Neural Networks

Despite the relentless pace of progress in computer architectures and the exponential growth in computational powers over the last few decades, there are still many problems that today’s computers can not solve. Some of these problems await the next generation of semiconductors to solve them. Others will likely remain beyond the reach of classical computers forever. The prospect of finally finding a solution to these “classically intractable” problems is setting people abuzz at the dawn of the era of Quantum Computing.

What is Quantum Computing?

Conventional computers operate with binary digits (bits) i.e they can have a definite state of either ‘0’ or ‘1’, Quantum Computers, on the other hand, have as its fundamental unit a quantum bit (qubit) which exploits quantum phenomena such as quantum superposition that allows the qubit to remain in an ambiguous(quantum) state between ‘0’ and ‘1’and quantum entanglement which makes a qubit influence another qubit’s state. The simultaneous ambiguity and co-ordination allow quantum computers to scale exponentially, doubling in capacity with each added qubit. This exponential scaling brings some NP problems, which otherwise might take millions of years to solve on even the most powerful classical computers, within the reach of quantum computers!

Quantum Annealing vs Universal Gate Quantum Computers

Developers of Quantum computers have taken different approaches and are using different materials to form qubits [2]. NTT Corporation has used photons as qubits [3], IonQ is developing trapped-ions based qubits [4]. Today’s state-of-the-art quantum computers, however, are made using super-conductors with D’Wave, IBM and Google leading the race. Architecturally, quantum computers can be found in two forms:

Quantum Annealers: The D-Wave machine is a quantum annealer running adiabatic quantum computing algorithms. This is great for optimizing solutions to problems by quickly searching over a space and finding a solution or for other applications such as sampling.

Universal Gate Quantum Computers: Manufactured by IBM and Google, a universal gate quantum computing system relies on building quantum circuit operations which sequentially perform operations on the qubits. These individual operations allow us to have better control over the transformations applied to qubits.

This design means that a universal gate quantum computer can perform several quantum algorithms that cannot directly(or efficiently) run on a quantum annealer, but this approach comes with its own challenges and a different design than a quantum annealer. D-Wave’s approach has allowed it to scale its system substantially.

Despite these restrictions on a Quantum Annealer it has many applications, from optimizing multivariable problems with unprecedented speed to quantum artificial intelligence (AI). In this article, we are exploring one such application where the training of Deep Neural Networks can benefit from Quantum Annealing using Deep Belief Networks.

Methodology

In Deep Learning, a well-known approach for training a Deep Neural Network starts by training a generative Deep Belief Network model, and then fine-tuning the weights using back-propagation or other discriminative machine-learning techniques. We test this method using a coarse-grained version of the MNIST digit data set[5].

The motivation behind this work comes from the basic principle of how Deep Belief Networks work. A Deep Belief Network is a stack of Restricted Boltzmann Machines, which is an unsupervised probabilistic deep learning model. These models are trained using the model’s “lowest energy configuration” which is fundamentally an intractable problem for classical computers. In most practical use-cases we make do with sub-optimal samples (using Gibb’s Sampling) and compensate by making several updates instead. However, now with quantum computers we do not need to bargain a trade-off and can expect rapid training on Deep Belief Networks. All else being equal, we are trying to see what improvements can sampling from Quantum Annealer offer compared to classical methods for pre-training.

Pre-Training Neural Networks with Deep Belief Networks

In general, in any model training exercise, instead of starting with randomly initialized weights, it is desirable to have the weights primed to our data set before-hand. Here, we train Deep Belief Networks in an unsupervised manner on the data set and use its weights as an initial point for our neural network. Such pre-training may help both in terms of optimization and in terms of generalization.

The entire process is undertaken in two stages:

1. Pre-training: Each layer of the Neural Network is treated as a Restricted Boltzmann Machine(RBM) and trained Greedy-Layer wise on the images. With samples drawn from either a classical computer or quantum annealer.

2. Discriminative Training: The images and labels are applied to the neural networks with 800 iterations (batch updates) of back-propagation.

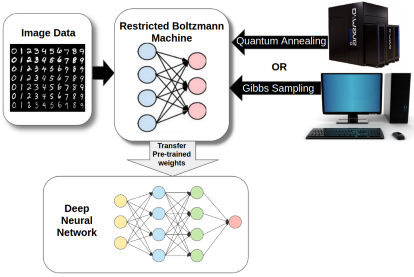
Figure 1: Pre-training with Restricted Boltzmann Machine

Performance Evaluation Metrics

Quantum Annealer’s hardware and its methods are fundamentally different from conventional CPU architecture. Therefore, we cannot draw a direct equivalence between these machines and pit a particular CPU chip against D’Wave’s Annealer. Therefore, benchmarking with ‘time taken to solve’ would not be reasonable. Instead, we compare the number of pre-training iterations(updates) taken by each of the methods to bring the model’s weights into a suitable range.

Model and its Data

It follows from the above that we need to build a model with layers that can individually be fitted on the quantum annealer for sampling. To cast the layer as an RBM on the annealer, we map each node in our RBM to a qubit.

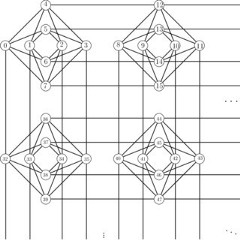
Figure 2: Qubit connectivity in D’Wave’s Annealer (Chimera graph)

Ideally, a 2000 Qubit annealer should easily be able to fit a 1000×1000 RBM, which is only possible when each qubit can directly interact with every other qubit. The qubits in D’Wave 2000Q, however, are sparsely connected [6], with each qubit connected to 6 other qubits only (Figure 2). Due to these restrictions, we are confined to a much smaller model. Each layer is afforded a size of 32×32 and we end up with a neural network of shape 32x32x32x10.

To bring the images of the MNIST dataset to a size of 32 pixels each, we first reduced the size of each image from a 28×28 pixels to a 6×6 pixels using pooling and then deleting corner pixels. We end up which a coarse-grained version of the images as shown in Figure 3.

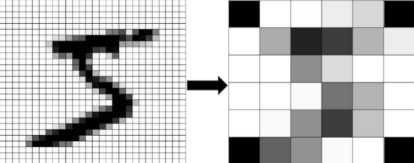
Figure 3: Coarse-Grained MNIST

To have a better idea about the whole process the dataset is broken into 10 parts (6000 images in each part) and trained 10 separate models on each part of the data set and collected its results.

Results

After the pre-training the models with quantum and classical approaches separately, we found that quantum annealer’s sampling took under 20 pre-training iterations to allow the models to be completely trained(after 800 iterations of back-propagation), whereas the classical approach took more than 60 iterations.

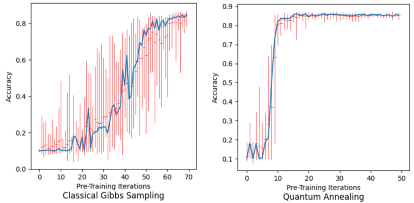
Figure 4: Training accuracy vs Pre-training Iterations

When this approach for pre-training with Quantum Annealers was first proposed in 2015 [1], a large number of samples were drawn from the Annealer with many techniques such as gauge transformation employed to have good enough samples to beat classical approaches. However, with recent improvements in noise reduction in D’Wave-2000Q Annealer, we only need to sample once with little or no dependence on other techniques.

Summary

When transferring any problem to Quantum Annealers we are still restrained by the number of qubits and the topological sparsity of the system. This however is rapidly changing, quantum computers are seeing exponential growth in their capacity[7] and are at the cusp of solving real-world problems.

At AlgoAnalytics (https://algoanalytics.com/) our many initiatives on Quantum Computing include building new tools, such as a Lagrangian relaxation program and other tools to simplify the process of formulating and encoding problems for the Quantum Annealer. With these tools, we have tackled several problems with potential real-world applications that might benefit greatly with speedups offered by quantum computers. Examples of these applications include finding the Optimal Arbitrage Opportunity or Vehicle Routing(Travelling Salesman Problem), both of which are NP-Hard Problems and would take an unfathomable amount of of time to solve on a conventional computer but can be efficiently solved using a Quantum Annealer.

For demo visit our link https://algoanalytics.com/demoapp